 |
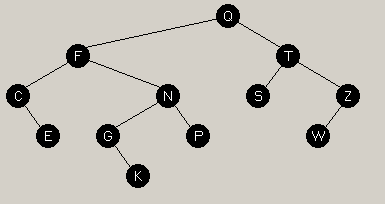
The first picture shows the initial tree created by inserting these letters in this order:
Q F T C N S Z E G P W K This is a valid AVL tree with 12 nodes and height 4. |
|
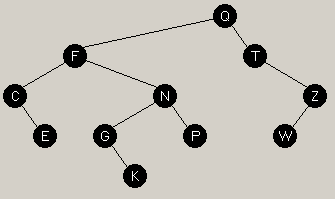 |
If you delete 'S', you get the picture on the left. Now, walking up the tree (to make sure all nodes are still balanced) we get to the first node, 'T', and see that it is out of balance. To balance it, we have to do 2 rotations. (It's a zig-zag situation.) | |
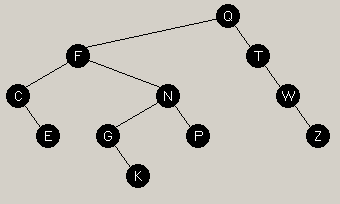 |
So, we rotate right about Z (promote node W), giving us the picture on the left. | |
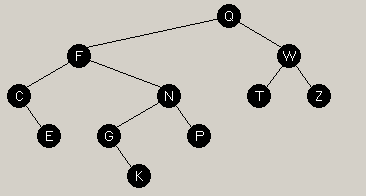 |
Then, we rotate left about T (promote node W again), giving us the picture on the left.
If we stopped here, we would see that the tree is still unbalanced at the root. The height of the left subtree rooted at node Q is 4 and the height of the right subtree rooted at node Q is 2. This node is not balanced. We discovered this as we continued up the tree. When we got to Q we realized that it was out of balance. The left subtree is heavy and is in a zig-zag orientation, so we have to perform another double rotation. In the diagram, y is Q, u is F, v is C, and w is N. |
|
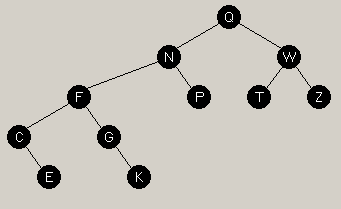 |
The first rotation is a left rotation about F (promoting node N), giving us the picture on the left. | |
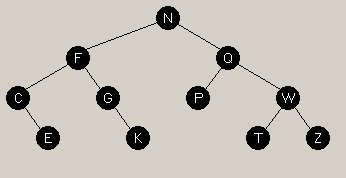 |
The second rotation is a right rotation about Q (promoting node N again), giving us the final picture
on the left.
This tree is now a valid, balanced AVL tree. |