B-Trees
- With in-memory data structures, the physical location in memory was a constant.
- What happens if the data structure is too large to fit into memory? Need to use external memory.
(e.g. hard disk)
- What is the definition of large?
- Essentially two types of memory in a computer
- Internal or primary storage: Fast, expensive, small amounts. Internal to the CPU. (Main memory)
- External or secondary storage: Slow, cheap, vast amounts. External to the CPU. (Hard disk)
- Main factors distinguishing slow/fast storage (disk/memory): Speed and Cost
- Cost today: RAM is about $5.00 per GB, Disk storage is about $0.025 per GB, and NAND SSD is about $0.11 per GB. (Summer 2021)
- Speed today: RAM is measured in ns (nanoseconds, a billionth of a sec), and hard disks are measured
in ms (milliseconds, a thousandth of a second). RAM access time is about 10 ns and hard disk access time
is about 10 ms. (Plus other factors, too).
- On average, it takes about 10 ms to access one byte from a hard disk.
- This includes seek time, latency, and transfer rate.
- Note that it takes about the same amount of time to access an entire sector (e.g. 512 bytes or more)
- This will have a direct effect on the data structures.
- On average, it takes about 1 microsecond (millionth of a second) to access a byte from main memory.
- All things considered, hard disks are about 10,000 times slower than RAM.
- Rotational velocity affects the times as well. (3600 rpm, 5400 rpm, 7200 rpm, 10K rpm, 15K rpm)
- SSDs are faster than spinning hard disks, but still extremely slow compared to RAM access.
- This means that data structures and algorithms that work fine for data in RAM won't work very well
for data on a disk.
It is true that the bottleneck in modern computers is main memory (RAM). But that's because we
assume that all of the data is already stored there. If you have to go to the disk, then
even slow RAM seems extremely fast compared to the disk.
Considerations:
- Programs designed for reading/writing data structures from/to external storage can bypass I/O overhead.
(i.e read sectors instead of files)
- All computations must be done in primary memory. (May further be required to be on the CPU itself.)
That's just the way computers work. Disks are for storage only.
- Must be able to fit some portion of the data into main memory for the algorithm to work.
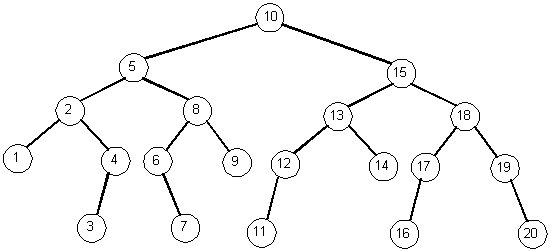
Suppose we have 20 data elements (keyed from 1 to 20) and we want to store them in a tree so we can minimize the search time (read: minimize the height).
Storing the data in a balanced binary tree: (Height: 4)
Storing the data in a 2-3 tree: (Height: 2)

Storing the data in a 2-3-4-5 tree: (Height: 1)

Storing the data in a tree that can have more than 20 children per node: (Height: 0)

Observations:
- As the number of children per node increases (or keys per node increases), the height decreases.
- This results in faster traversals (depending on traversal speeds), or larger trees with smaller height.
- The maximum number of children per node is called the branching factor (or fanout) of the tree.
- BSTs have a branching factor of 2.
- 2-3-4 trees have branching factor of 4. (Worst case: O(log2N), Best case: O(log4N), base is a constant)
- Trees with large branching factors tend to be very shallow (not deep).
- Maximizing the branching factor is the key (no pun intended) to the efficiency of B-Trees.
- We've actually just traded one search mechanism for another.
- In a binary tree, we spend a lot of time following left and right child pointers.
- In an n-ary tree (like the trees above), we spend a lot of time finding keys in the nodes.
- This is exactly how the BList worked where we had many elements per node.
- With 2048 elements per node, we achieved more than 100X speedup.
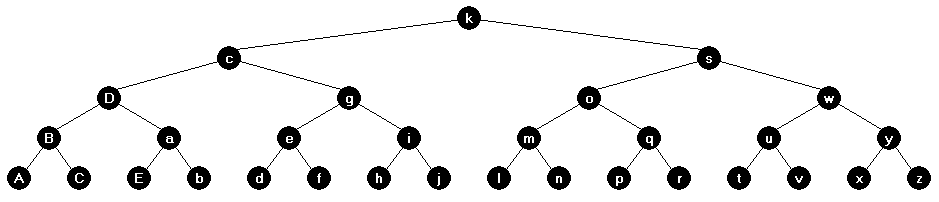
For a balanced binary tree, the height, h was based on the number of nodes/elements: (1 element per node)
h = floor(log2(N))
So, a full and complete balanced binary tree with 31 nodes/elements will have a height of 4:
In a balanced n-ary tree, the height is also based on the number of elements: (more than 1 element per node)
h = floor(logbf(N)) where bf is the branching factor. (Note this is the minimum height)
So, a balanced 2-3-4 tree with 15 elements will have a height of 1. The same tree with 16 elements will
have a height of 2 (the root node splits causing the tree to add one more level).

| Same data in a balanced binary tree (height is 3): | Showing the "4-nodes"
(if this was a red-black tree): |
|---|

|

|
- Named by Bayer and McCreight who studied them in 1972.
- Used primarily for external searching.
- Based on multi-way trees (2-3, 2-3-4, etc.)
- Each node in a B-Tree of order M has between M and M/2 children, except the root.
- All nodes, except the root, are at least half full.
- The BList shows this.
- A BST has a branching factor of 2 (which is also the base of the lg used in complexity computations).
- A B-Tree's height grows logarithmically with the number of nodes it contains. (The base of lg is the branching factor).
Discussion of other Trees
More Details about B-Trees:
- All leaf nodes are at the same level. (Like 2-3-4 trees)
- An internal node with N children has N - 1 keys.
- Typically, an internal node has an array of N - 1 keys and an array of N pointers.
- The structure of a leaf node may be different than an internal node.
- The nodes are page-based for optimal performance (determined by the hardware, e.g. hard drive sector/cluster size), which means
the number of keys/children in a node is directly related to the size of a page on disk. (Disk pages are similar
to memory pages used by a memory manager.)
- Think about data alignment in memory.
Below is a diagram of a B-tree of height 2 containing over one billion keys. Each internal node and leaf contains 1000 keys.
There are 1001 nodes at depth 1 and over one million nodes at depth 2. There are over 1 billion keys at level 2.
Shown inside each node is the number of keys in the node.
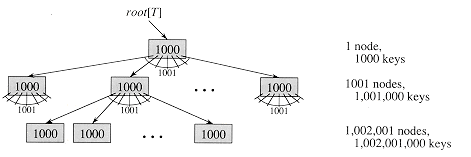
© 2001 Cormen et al.
Suppose the entire tree fit into memory. What can you say about the algorithm used
to find a particular value? What if we had a balanced BST instead? What about the performance?
Self-check: What is a tree's branching factor? What is the branching factor of
a BST? A 2-3 tree? A 2-3-4 tree? At most, how many children does a B-tree of order M have?
When storing the data in the node, a node may contain:
- The number of keys in the node
- A sorted array of keys
- A boolean flag indicating if the node is a leaf or not (may be implicit based on depth of the node)
- An array of pointers to children (the keys separate the ranges of the children)
- A variation of the B-Tree is the B+-Tree, which stores the data outside of the node.
This maximizes the branching factor because more pointers (therefore, more children) can be stored in a single node.
Number of Keys and Children
- There is a lower and upper bound on the number of keys a node can contain.
- The minimum number of children a node can contain is the minimum degree of the tree.
- The minimum degree of a tree is denoted as t, and t ≥ 2
- A 2-3-4 tree has minimum degree t = 2. Most B-Trees have a (relatively) large value of t.
- The general formula for the height (maximum) of a balanced tree replaces 2 with the minimum degree, t:
h ≤ floor(logt(N))
This leads to:
floor(logbf(N)) ≤ h ≤ floor(logt(N))
- Reminder: bf is the branching factor, which is the maxiumum number of children.
- A variation of the B-Tree is the B*-Tree,
which requires each node to be 2/3 full instead of half full.
(When nodes are full, share with neighbors. Cheaper than splitting.)
struct Data1
{
int Key; // 4 bytes
int Foo; // 4 bytes
int Bar; // 4 bytes
};
struct BTreeNode
{
int NumKeys; // num keys in this node
Data1 Keys[MAX_KEYS]; // key is in a struct
BTreeNode *Children[MAX_CHILDREN]; // "pointers" to children
// MAX_CHILDREN == MAX_KEYS + 1
};
Given a PAGE SIZE of 4096 bytes, this would yield:
- Max keys: 255 (4088 / 16)
- Max children (Max keys + 1, branching factor, order): 256
- Min children (minimum degree, t): 128
- Min keys (Min children - 1): 127
Diagrams
Suppose this was our data: (52 bytes)
struct Data2
{
int Key; // 4 bytes
int Foo; // 4 bytes
int Bar; // 4 bytes
char Name[20]; // 20 bytes
double This; // 8 bytes
double That; // 8 bytes
float Other; // 4 bytes
};
Given the same PAGE SIZE of 4096 bytes, this would yield:
- Max keys: 73 (4088 / 56)
- Max children (Max keys + 1, branching factor, order): 74
- Min children (minimum degree, t): 37
- Min keys (Min children - 1): 36
What about this data:
struct Data3
{
int Key; // 4 bytes
int Data; // 4 bytes
};
Given the same PAGE SIZE of 4096 bytes, this would yield:
- Max keys: 340 (4088 / 12)
- Max children (Max keys + 1, branching factor, order): 341
- Min children (minimum degree, t): 170
- Min keys (Min children - 1): 169
Self-check: What is a B-tree's minimum degree? What is the minimum
degree of a 2-3-4 tree?
- Operations have to account for disk access.
- Data may not be in memory, so must be retrieved from disk (algorithms only run in memory/CPU).
- Typically, some kind of manager handles the disk access (read a node, write a node).
- Disk access is transparent to the client (via an API).
- Remember, the children pointers in a node are pointers to disk blocks.
- B-Trees facilitate key-range searches. (This is what databases are good at.)
For example:
- Find all data with keys: 100 ≤ key ≤ 200.
- Find all students with a GPA between 3.1 and 3.8.
- Not as easy to do with a BST.
Inserting a key/data value
- Similar to 2-3-4 trees; insert at the appropriate leaf and update count (NumKeys).
- Need to insert key/data into sorted array. Complexity? (This is CPU complexity)
- If leaf is full, need to split:
- Middle key goes to parent
- Remaining keys get split into 2 nodes
- Like 2-3-4 trees, we can split full nodes on the way down during insert operation.
Advantage of splitting on the way down?
- Splitting the root causes the height to grow by 1.
Deleting a key/data value
- Delete from a leaf, decrement the count (NumKeys)
- Can be complicated if a node ends up having less than the minimum number of keys.
- Need to "adjust" the tree to satisfy B-Tree requirement.
- We can "borrow" from a neighboring node, but what if neighbor can't spare any?
(Works like deletion in a 2-3-4 tree, merge nodes)
- Can allow nodes to become "underfull". In practice, this is generally acceptable.
- May "fix" the tree offline.
- Another scheme may just mark the data as deleted (lazy delete) instead of using costly merges.
- Eventually a new tree will be constructed (offline) when the performance decreases due
to many marked items.
- We saw this scheme with open-addressed hash tables. The marked slots were removed the
next time we resized the table.
- All data is stored outside of the nodes.
- Branching factor is maximized
- Used quite often in practice
- Allows for multiple representations (sortings) on the same data. Each B+ tree has the
same pointers to the actual data.
- This is a huge win and keeps the data normalized.
- This could be done with binary search trees or other node-base containers.
The size of DATA below is 1344. With 4096 byte pages, we would only get 3 structs per page.
struct DATA
{
int ID; // the key
char Name[32];
struct
{
double x;
double y;
double z;
} Position;
double NFA[128];
int DFA[64];
};
A good candidate for a B+ tree implementation.
File systems (huge amounts of data) such as
NTFS (Windows),
APFS (macOS),
JFS,
XFS,
ReiserFS, and
Btrfs
are implemented using B+Trees. Also, Microsoft's SQL Server and Oracle's
database systems support B+Trees.
Filesystem notes
More information about B-Trees at
wikipedia.
