Recursive Algorithms and Functions

Recursive Algorithms

A recursive algorithm is simply one that is defined in terms of itself. Some examples:

Natural Numbers

1 is a Natural Number
The successor of any Natural Number is a Natural Number

In C/C++ code:

bool IsNatural(int number)
{
  if (number == 1)
    return true;
  else
    return IsNatural(number - 1);
}

Call stack for IsNatural(5):

IsNatural(int 1) line 127   <--- base case stops the recursion
IsNatural(int 2) line 132 + 12 bytes
IsNatural(int 3) line 132 + 12 bytes
IsNatural(int 4) line 132 + 12 bytes
IsNatural(int 5) line 132 + 12 bytes
main() line 335 + 12 bytes
mainCRTStartup() line 206 + 25 bytes
KERNEL32! 7c4e87f5()

Terminology

Recursive call - A function call in which the function being called is the same as the one making the call.
Recursive definition - A definition in which something is defined in terms of smaller versions of itself.
Base case - The case for which the solution can be stated non-recursively.
General case (recursive case) - The case for which the solution is expressed in terms of a smaller version of itself.
Recursive algorithm - A solution that is expressed in terms of (a) a base case and (b) a recursive case.
Infinite recursion - The situation in which a function calls itself over and over endlessly.

Recursive functions can call themselves either directly or indirectly:

Direct - FunctionA calls FunctionA
Indirect - FunctionA calls FunctionB, FunctionB calls FunctionA or FunctionA calls FunctionB, FunctionB calls FunctionC, FunctionC calls FunctionA.

Reasons for creating subproblems:

The subproblems are smaller or simpler than the original problem.
The subproblem has an immediate solution, or can be solved by further recursion.
The results of the subproblems can be combined to give the overall solution to the original problem.

The splitting of larger problems into smaller ones is known as the Divide and Conquer strategy. (You've been using a form of this strategy in all of your programming.)

Other Examples

BNF Grammars (Backus-Naur Form):

<expression> ::= <number> | <number> <operator> <expression>
<number> :: = <digit> | <digit> <number>
<digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<operator> ::= + | - | * | /

Some example expressions:

5
3 + 5
12 / 7
6 - 14 * 11

A classic example is the definition of factorial. To calculate N! for all values >= 0:

If N = 0 then N! = 1
If N > 0 then N! = N * (N - 1)!

Expanded general form:

N! = N * (N - 1) * (N - 2) * ... * 2 * 1

Expanded example:

5! = 5 * 4!
   = 5 * (4 * 3!)
   = 5 * (4 * (3 * 2!))
   = 5 * (4 * (3 * (2 * 1!)))
   = 5 * (4 * (3 * (2 * (1 * 0!))))   (we've hit the base case)
   = 5 * (4 * (3 * (2 * (1 * 1))))
   = 5 * (4 * (3 * (2 * 1)))
   = 5 * (4 * (3 * 2))
   = 5 * (4 * 6)
   = 5 * 24
   = 120

Some other values:

0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800

Recursion and Function Calls

Looping can be accomplished in C++ by:
- while
- for
- do . . . while
Another way—recursion
a function calling itself (either directly or indirectly)
this is a form of repetition (looping)
infinite loop unless a stop condition is included in the algorithm (must have a terminating condition)
In mathematics we sometimes call these recurrence relations
Recursion is not unique to C++; many languages support it

Basic Idea

Figure out the pattern of repetition that calls the recursive function.
Find out what changes in the parameters to cause the problem to change with each recursive call.
Figure out the base case or trivial case; this is what stops the recursion.

More Recursion Details

Looking again at the factorial function defined recursively:

N! = N · (N - 1)!

This function assumes that N >= 1 and by definition 0! = 1. This function is recursive because it is defined in terms of itself. The traditional way of writing recursive definitions is like this:

0! = 1           	 base case 
N! = N · (N - 1)!	 recursive case

For example, 5! is defined like this:

5! = 5 · 4!

And 4! is defined like this:

4! = 4 · 3!

And so on:

3! = 3 · 2!
2! = 2 · 1!
1! = 1 · 0!
0! = 1		 this is the base case

Which ultimately gives us:

5 · 4 · 3 · 2 · 1 · 1 = 120

Sample code

Pseudo-assembly

Another popular function that is defined recursively is the power function:

X^N = X · X^{(N - 1)}

This function assumes that N > 0 and by definition X⁰ = 1. We would write the recursive definition like this:

X⁰ = 1            base case 
X^N = X · X^{(N - 1)}  recursive case

Sample code

Find the maximum value in a list of integers recursively. (Don't use this method in an actual project!)

Base: MaxVal([x]) = x

Recursive:
MaxVal([a₁, a₂, a₃, ..., a_N]) = if a₁ > MaxVal([a₂, ..., a_N]) then 
                                   a₁
                                else 
                                   MaxVal([a₂, ..., a_N])

Best case: O(n) (Sorted high to low)
Worst case: O(2ⁿ) (Sorted low to high)

Sample code

Tracing Function Calls

Given the 3 functions as defined below:

int f1(int a, int b) { int x, y; x = f2(a); y = 4 + b; return x + y; }

int f2(int x) { int a, b, c; a = x; b = 5; c = f3(a + b); return c; }

int f3(int x) { int a; // snapshot taken before // this line executes: a = x * 3; return a; }

What does the following program print?

void main(void)
{
  int x;
  float f;

  f = 2.7;
  x = f1(2, 3);

  cout << x << endl;
}

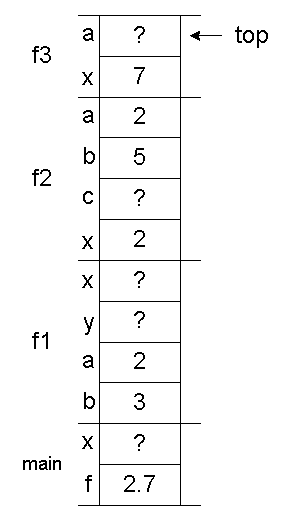
This image below is a "snapshot" of what the runtime stack (memory) looks like just before the statement

a = x * 3;

in f3 is executed. (Actually, it's a little more complicated than this, but it gets the point across.)

int f1(int a, int b)
{
  int x, y;

  x = f2(a);
  y = 4 + b;


  return x + y;
}

int f2(int x)
{
  int a, b, c;

  a = x;
  b = 5;
  c = f3(a + b);

  return c;
}

int f3(int x)
{
  int a;

  // snapshot taken before
  // this line executes:
  a = x * 3;     

  return a;
}

The "stack" and Recursive Programming

Each function's portion of the stack is called an activation record or stack frame
The stack grows and shrinks during program execution.
This is why local variables are undefined and are called automatic variables
Global data and dynamically allocated data (and static variables in C++) are created on the heap, so they stay around for the life of the program (or until you delete them.)
Can you see why "infinite recursion" will cause bad things to happen? What thing exactly?
The runtime stack is what enables recursion to work without any programmer intervention.

Given this recursive definition of Print:

void Print(const int *list, int first, int last)
{
  if (first <= last)
  {
    cout << list[first] << endl;
    Print(list, first + 1, last);
  }
}

We can print the second, third, and fourth integers in the array using this syntax:

Print(list, 1, 3)

Write another version to print a "section" of the array. This function should only take 2 parameters: A pointer to an array and the number of elements to print.

Simple simulation

Reverse a list of integer recursively:

void PrintRev1(const int *list, int first, int last)
{
  if (first <= last)
  {
    PrintRev1(list, first + 1, last);
    cout << list[first] << endl;
  }
}

Reverse a list of integers iteratively using a stack:

void PrintRev2(const int *list, int first, int last)
{
  std::stack<int> s;
  while (first <= last)
    s.push(first++);

  while (!s.empty())
  {
    cout << list[s.top()] << endl;
    s.pop();
  }
}

Reversing Strings

Here's a very simple function that reverses a range of characters in a string:

void ReverseStringIt(char *s, int from, int to)
{
  char c;
  while (from < to)
  {
      // Swap the edges first   
    c = s[from];
    s[from] = s[to];
    s[to] = c;

      // Advance the "edge pointers"   
    from++;
    to--;
  }
}

Simple usage:

char p[] = "123456789";

ReverseStringIt(p, 0, 8);  //987654321 
ReverseStringIt(p, 0, 3);  //432156789 
ReverseStringIt(p, 3, 7);  //123876549

Implementing a recursive version:

void ReverseStringRec(char *s, int from, int to)
{
  char c;
  if (from < to)
  {
      // Swap the edges   
    c = s[from];
    s[from] = s[to];
    s[to] = c;

      // Reverse the "internal" characters   
    ReverseStringRec(s, from + 1, to - 1);
  }
}

Write a recursive function that can reverse a singly-linked list in-place. Use the Node struct and function prototype below.

struct Node
{
  Node *next;
  int data;
};

void ReverseListRec(Node*& list, Node *prev); // Recursively reverse list in-place

Fibonacci Example

For all values of n > 1, we have the Fibonacci numbers defined recursively as:

F₀ = 0             base case
F₁ = 1             base case
F_N = F_n-1 + F_n-2    recursive case

So the first 10 Fibonacci numbers are: 0, 1, 1, 2, 3, 5, 8, 13, 21, and 34.

Implementing this iteratively causes the "elegance" to get lost:

int IterFibonacci(int number)
{
  if (number == 0)
    return 0;
  else if (number == 1)
    return 1;
  else
  {
    int v1 = 1, v2 = 0;
    for (int i = 2; i <= number; i++)
    {
      int temp = v1;
      v1 += v2;
      v2 = temp;
    }
    return v1;
  }
}

What's the complexity of the iterative function above? How many times does the for loop iterate?

Now, implementing it recursively from the definition is trivial and almost writes itself:

int RecFibonacci(int number)
{
  if (number == 0)       // F₀ = 0
    return 0;
  else if (number == 1)  // F₁ = 1
    return 1;
  else                   // F_N = F_n-1 + F_n-2
    return RecFibonacci(number - 1) + RecFibonacci(number - 2);
}

What's the complexity of the recursive function above? How many times is the function called for a given number?

To help you really see how bad this is, we can build the execution tree:

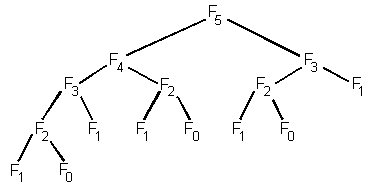
The parent/child relationship has the meaning:

"To calculate the parent, we have to calculate the children first."

So, to compute F₅, we need to first compute F₄ and F₃. But, in order to compute F₄, we need to compute F₃ and F₂, etc.

This table shows the number of times the RecFibonacci function is called for each value:

Number    F₀   F₁   F₂   F₃   F₄   F₅   F₆   F₇   F₈   F₉   

Value     0    1    1    2    3    5    8   13   21   34         
Calls     1    1    3    5    9   15    25  41   66  108

For example, the number of calls to RecFibonacci to evaluate F₇ is 41. This is because it evalutes F₆ (25 calls) and F₅ (15 calls) plus the original call for F₇. This implementation has Fibonacci complexity.