The bubble sort algorithm is a very simple algorithm to understand and to implement. It works great on small lists but is very inefficient on large lists.
A bubble sort works by comparing adjacent items and exchanging them if they are out of order. The meaning of "out of order" depends on how you want the items sorted: smallest to largest, or largest to smallest.
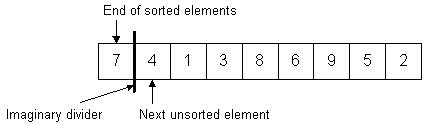
For example, suppose we have this list of numbers that we want to order from smallest to largest:
The final list should look like this:7 4 1 3 8 6 9 5 2
Using the bubble sort algorithm, we simply compare two items at a time, swapping them if the left one is larger than the right one. (We want them ordered from small to large). Starting with the first two items:1 2 3 4 5 6 7 8 9
7 is larger than 4, so we swap them:7 4 1 3 8 6 9 5 2 ^ ^
Next, we compare items 2 and 3 and find that 7 > 14 7 1 3 8 6 9 5 2 ^ ^
so we swap them:4 7 1 3 8 6 9 5 2 ^ ^
You can see that 7 > 3 as well:4 1 7 3 8 6 9 5 2 ^ ^
4 1 7 3 8 6 9 5 2
^ ^
4 1 3 7 8 6 9 5 2
^ ^
4 1 3 7 8 6 9 5 2
^ ^
4 1 3 7 8 6 9 5 2
^ ^
4 1 3 7 6 8 9 5 2
^ ^
More importantly, after this pass through the list, the value 9 is now in its proper position.4 1 3 7 6 8 5 2 9
Source code for bubble sort:
void BubbleSort(int a[], int size)
{
for (int i = 0; i < size - 1; i++)
for (int j = 0; j < size - i - 1; j++)
if (a[j] > a[j + 1])
Swap(a[j], a[j + 1]);
}
You'll notice that the list was actually sorted after the 7th (i == 6) iteration, so we have a few unecessary iterations. We can add a little code to break out of the loop early, if we detect that the list is sorted.4 1 3 7 6 8 5 2 9 i == 0 1 3 4 6 7 5 2 8 9 i == 1 1 3 4 6 5 2 7 8 9 i == 2 1 3 4 5 2 6 7 8 9 i == 3 1 3 4 2 5 6 7 8 9 i == 4 1 3 2 4 5 6 7 8 9 i == 5 1 2 3 4 5 6 7 8 9 i == 6 <=== already sorted 1 2 3 4 5 6 7 8 9 i == 7 1 2 3 4 5 6 7 8 9 i == 8
void BubbleSort(int a[], int size)
{
for (int i = 0; i < size - 1; i++)
{
int swaps = 0;
for (int j = 0; j < size - i - 1; j++)
{
if (a[j] > a[j + 1])
{
Swap(a[j], a[j + 1]);
swaps = 1;
}
}
// If we didn't swap any item, the list must be sorted
// and we can stop the algorithm now.
if (swaps == 0)
break;
}
}
Source code for a helper function to swap two integers:
void Swap(int &a, int &b)
{
int temp = a;
a = b;
b = temp;
}
The idea behind the insertion sort is that you start with a sorted list and continually insert the next element into its proper position in the sorted list. Sounds like a chicken-or-the-egg thing, but it's not. So, how do we start with a sorted list (since that's our end goal)? Simple, we consider the first element in the unsorted list to be a list of one. By definition, a list with only one element is already sorted. (Think about it.) So, what we have is our original list that is partitioned into two lists: a sorted portion and an unsorted portion. The sorted portion is in the front of the list, and the unsorted portion is in the back of the list. For example, if we have 9 elements in our list, the sorted portion consists of the first element (in the front) and the unsorted portion consists of the remaining 8 elements (at the end).
Now, we simply take each element (one-at-a-time) from the unsorted portion, and insert it into its proper position in the sorted portion. For example, suppose we have an array of numbers (same as before):
This is how we would see our "partitioned" array at the start of the sort:7 4 1 3 8 6 9 5 2

Following the logic described above, we take the next element from the unsorted portion and insert it into the correct position in the sorted portion. This is done by:
Make a copy of the next unsorted element, which is 4:
7 is larger than 4, so copy it to the open slot:
We've run out of sorted elements so put 4 in the open slot at the front:
Now, we have 2 elements in the sorted portion and 7 elements in the unsorted portion. The next unsorted element is 1, so we perform the same steps using 1 as X:
Make a copy of the next unsorted element, which is 1:
7 is larger than 1, so copy it to the open slot:
4 is larger than 1, so copy it to the open slot:
We've run out of sorted elements so put 1 in the open slot at the front:
Now, we can start to see how our sorted portion is being constructed. We have 3 elements (in sorted order) in the left portion, and 6 elements remaining in the right (unsorted) portion.
Make a copy of the next unsorted element, which is 3:
7 is larger than 3, so copy it to the open slot:
4 is larger than 3, so copy it to the open slot:
1 is not larger than 3, so we copy 3 to the open slot:
We now have 4 elements in the sorted portion with 5 remaining to be inserted.
Make a copy of the next unsorted element, which is 8:
7 is not larger than 8, so we copy 8 to the open slot: (It turns out that 8 was already in the correct position, but we didn't know that until we looked at the element to the left.)
We now have 5 elements in the sorted portion with 4 remaining to be inserted.
Make a copy of the next unsorted element, which is 6:
Shift larger elements to the right (7 and 8):
Place 6 in the open slot:
We now have 6 elements in the sorted portion with 3 remaining to be inserted.
9 is in the correct position already, so we have 7 sorted elements and 2 remaining:
Make a copy of the next unsorted element, which is 5:
Shift larger elements to the right (6, 7, 8, and 9):
Place 5 in the open slot:
Now we have 8 sorted elements and one remaining:
Make a copy of the next unsorted element, which is 2:
Shift larger elements to the right (3, 4, 5, 6, 7, 8, and 9):
Place 2 in the open slot:
There are no more elements in the unsorted portion, so the list is sorted.
Source code for insertion sort:
// Sort by repeatedly taking the next item and inserting it
// into the final data structure in its proper order with
// respect to items already inserted.
//
// Sorting can be done in place by moving the next item into place by
// repeatedly swapping it with the preceding item until it is in place
void InsertionSort(int a[], int size)
{
for (int i = 1; i < size; i++)
{
int j = i;
int current = a[i];
// Shift all elements left of current
// that are greater than current.
// Shifting them to the right. e.g.:
// 5 is the item to insert:
// 123478592 becomes 1234 7892
// ^
while ((j > 0) && (a[j-1] > current))
{
a[j] = a[j-1];
j--;
}
// Then insert current value in open slot
// 123457892
// ^
a[j] = current;
}
}
Selection sort is probably the most intuitive sort because it mimics how people think. The algorithm is straight-forward:
1 was found to be the smallest, so it is swapped with the value stored at the
current position (the first slot)
Move the current position to the right one and scan for the next smallest value.
2 is the smallest, so swap it with 4.
Move the current position to the right one and scan for the next smallest value.
3 is the smallest, so swap with 7.
Continue the process until the last position is reached.
Source code for selection sort:
// Sorting can be done in place by swapping the least remaining item with the
// item in the next position to be filled.
void SelectionSort(int a[], int size)
{
for (int i = 0; i < size; i++)
{
int min = i;
int j;
// Find the smallest element in the unsorted list
// (Linear search)
for (j = i + 1; j < size; j++)
if (a[j] < a[min])
min = j;
// Swap the smallest unsorted element with
// the last element in the sorted list.
Swap(a[min], a[i]);
}
}
I added a bubble sort and insertion sort to the vector labs. There was already a selection sort.
The size of the list was 10,000 items.
N(N - 1) 10,000(9999) 99,990,000
0 + 1 + 2 + 3 ... + N - 1 = -------- = ------------ = ---------- = 49,995,000
2 2 2
WORST (Sorted in reverse) - Selection sort is better than average with reverse sorting.********** TestSelectionSortStress ********** Sorted: compares = 49995000, swaps = 0 1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 ********** TestBubbleSortStress ********** Sorted: compares = 49995000, swaps = 0 1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 ********** TestInsertionSortStress ********** Sorted: compares = 9999, swaps = 0 1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192
The worst case swaps is interesting because, after half of the elements have been swapped, the entire array is sorted! That's because the array is symmetrical and when you swap the "ends", you are putting items in their correct location. Didn't notice this until I wrote a program that "proved" it.
AVERAGE (Random distribution) - Selection sort is worse with random data than with reverse sorting.********** TestSelectionSortStress ********** Sorted: compares = 49995000, swaps = 5000 2 3 5 9 17 33 65 129 257 513 1025 2049 4097 8193 ********** TestBubbleSortStress ********** Sorted: compares = 49995000, swaps = 49995000 2 3 5 9 17 33 65 129 257 513 1025 2049 4097 8193 ********** TestInsertionSortStress ********** Sorted: compares = 50004999, swaps = 49995000 2 3 5 9 17 33 65 129 257 513 1025 2049 4097 8193
********** TestSelectionSortStress ********** Sorted: compares = 49995000, swaps = 9987 4 4 7 10 17 34 71 116 247 505 990 1979 4067 8187 ********** TestBubbleSortStress ********** Sorted: compares = 49995000, swaps = 25228071 1 2 5 7 19 38 70 130 262 494 974 2018 4091 8184 ********** TestInsertionSortStress ********** Sorted: compares = 24943433, swaps = 24933434 3 4 5 12 21 42 81 150 268 509 1010 2075 4053 8153
Perfect partitioning.
The array is sorted after 3 partitioning steps. (log2 8)
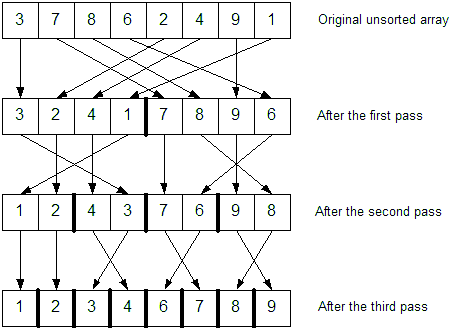
Question: How would this algorithm work for linked lists?
http://en.wikipedia.org/wiki/File:Sorting_quicksort_anim.gif