2-3-4 Tree Delete Example

Deleting Elements from a 2-3-4 Tree

Deleting an element in a 2-3-4 tree assumes we will grow (merge) nodes on the way down.

The idea is intuitive, but writing the algorithm down in English seems to make it look/sound harder than it is.

Again, when dealing with trees, there are different cases. Here, there are 3 different cases:

  1. If the element, k is in the node and the node is a leaf containing at least 2 keys, simply remove k from the node.

  2. If the element, k is in the node and the node is an internal node perform one of the following:
    1. If the element's left child has at least 2 keys, replace the element with its predecessor, p, and then recursively delete p.
    2. If the element's right child has at least 2 keys, replace the element with its successor, s, and then recursively delete s.
    3. If both children have only 1 key (the minimum), merge the right child into the left child and include the element, k, in the left child. Free the right child and recursively delete k from the left child.

  3. If the element, k, is not in the internal node, follow the proper link to find k. To ensure that all nodes we travel through will have at least 2 keys, you may need to perform one of the following before descending into a node. Then, you will descend into the corresponding node. Eventually, case 1 or 2 will be arrived at (if k is in the tree).
    1. If the child node (the one being descending into) has only 1 key and has an immediate sibling with at least 2 keys, move an element down from the parent into the child and move an element from the sibling into the parent.
    2. If both the child node and its immediate siblings have only 1 key each, merge the child node with one of the siblings and move an element down from the parent into the merged node. This element will be the middle element in the node. Free the node whose elements were merged into the other node.
Also, much like when deleting from a binary tree, all deletions are actually done at the leaf level, meaning that Case #1 is the way all items are actually deleted from the tree. We may have to push elements down into the leaves before actually deleting them.
  1. Given this tree:

    2. We are going to delete the nodes in this order: A N H R C P E F V B X Y S Z. Deleting the nodes in this order will demonstrate each of the possible cases above.

  2. Deleting A is Case #1: A is in a leaf and there are at least 2 keys in the node.


  3. This is the simplest case: Just remove A from the node, resulting in this tree:

  4. Deleting N is Case #3.1: N is in a leaf node, and it is the only key in the node.


  5. There are at least 2 keys in the sibling node, so move the right-most key to the parent, and move the right-most parent down.


  6. Now There are 2 keys in the leaf node, which is case #1. Just delete N, resulting in this tree:

  7. Deleting H is case #3.2: H is in a leaf node, and there are no siblings with at least 2 keys.


  8. The parent has at least 2 keys, so we merge the right-most parent with its children:


  9. Now we can simple delete H from the leaf node, resulting in this tree:

  10. Deleting any key from a leaf node will first require that we merge the root, P with its two children (C and V) because of the "merge on the way down" rule.


  11. After merging the root with its children:

  12. Now we can proceed to delete R, which is case #1, R is in a leaf node and there are at least 2 keys in the node:


  13. After deleting R, the resulting tree looks like this:

  14. Deleting C is case #2.2: C is in an internal node, and its right child has at least two keys:


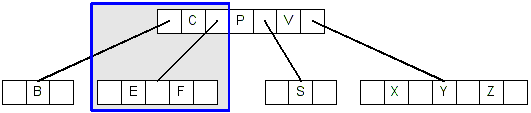
  15. We replace C with its successor, which is E:


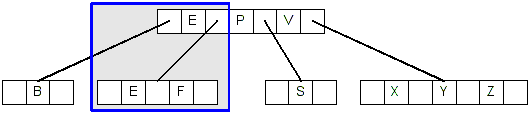
  16. Now we continue the search looking for E. Since E is in a leaf node and there are at least 2 keys in the node, we just delete E, resulting in this tree:

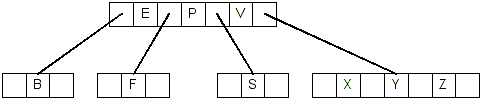
  17. Deleting P is case #2.3. P is in an internal node, and both of its children only have a single key:


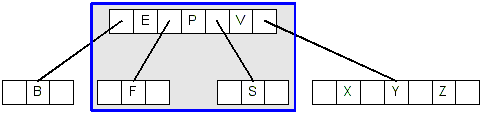
  18. So we merge P with its children. Now P is in a leaf node which has at least 2 keys:


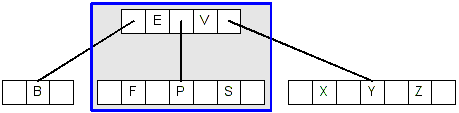
  19. Now we can simply delete P, yeilding this tree:

  20. Deleting E is case #2.2: E is in an internal node and its right childe has at least 2 keys, so we replace E with its successor, F.


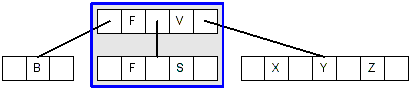
  21. Now we can delete the original F because it is in a leaf node that contains at least 2 keys, resulting in this tree:

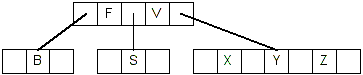
  22. Deleting F is case #2.3. F is in an internal node, and both of its children only have one key:


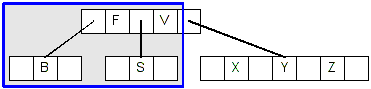
  23. So we merge F with its children, giving us this tree:


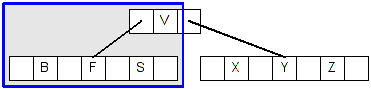
  24. Now, F is in a leaf node that has at least 2 keys, so we simply delete F:

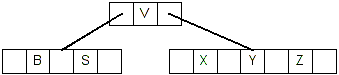
  25. Deleting V is case #2.1. V is in an internal node, and its left child has at least 2 keys:


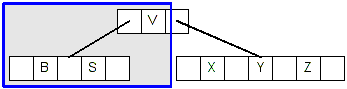
  26. So, we replace V with its predecessor, which is S:


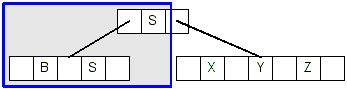
  27. Now we delete the original S because it is in a leaf node that has at least 2 keys, resulting in this tree:

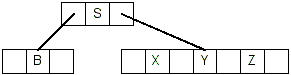
  28. Deleting B is case #3.1. B is in a leaf that has only 1 key, but its sibling has at least 2 keys:


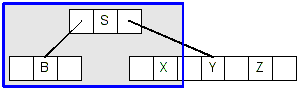
  29. So we replace the parent key, S, with S's successor, X, and move S into its left child, giving us this tree:


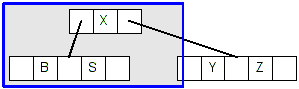
  30. Now, the node with B has at least 2 keys and is a leaf node, so we can simply delete B resulting in this tree:

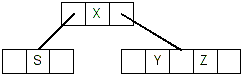
  31. Deleting X is case #2.2, X is in an internal node, and there is at least 2 keys in its right child:


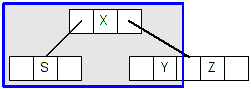
  32. So we replace X with it's successor, Y:


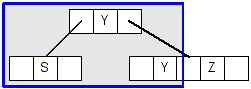
  33. Now we can delete the original Y because it is in a leaf that has at least 2 keys, giving us this tree:

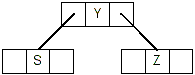
  34. Deleting Y is case #2.3. Y is in an internal node and both of its children have only 1 key:

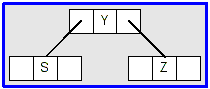
  35. Merging Y (the root) with its children gives us this tree:

  36. Now, deleting Y (which is case #1) yields this tree:

  37. Since we have only one node, which is a leaf, deleting S is case #1, and gives us this tree:

  38. Finally, deleting Z is also case #1 and yields an empty tree.