Introduction to Trees

|
|
0 if node is a root level(parent) + 1 if node is a child of parent
1. The height of a tree is the length of the longest path from the root to a leaf.These are all trees.
2. The height is the maximum of the levels of the tree's nodes.
This is not a tree. (Y has 2 parents)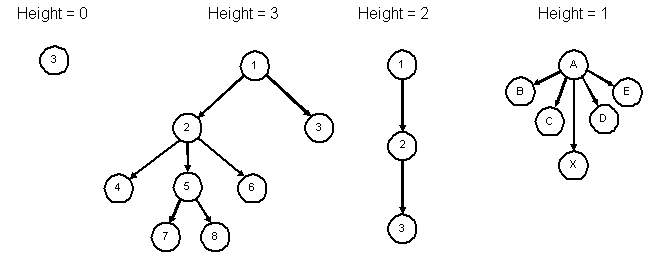
Don't confuse the size of a tree with the height of a tree. The size is simply the number (count) of nodes in the tree.
Binary Trees
A binary tree is a collection of nodes such that:
Representing binary trees with diagrams: sometimes an empty box is used to indicate an empty child (empty subtree). The squares are external nodes (leaves) and the circles are internal nodes. These diagrams are referred to as extended binary trees:
| A binary tree | An extended binary tree |
|
|
|---|
A balanced binary tree (height-balanced) is a tree where for each node the depth of the left and right subtrees differ by no more than 1.
| A balanced binary tree | An unbalanced binary tree |
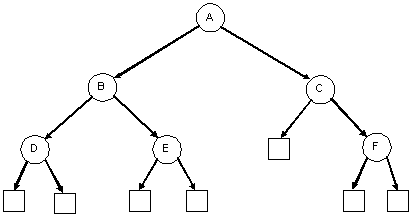
|
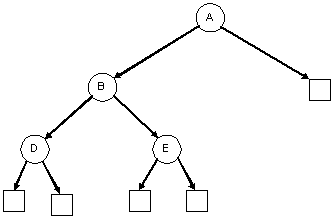
|
|---|
| A degenerate binary tree | A balanced binary tree (it's also a complete binary tree) |
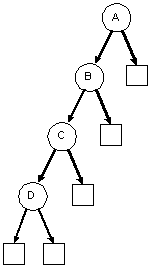
|
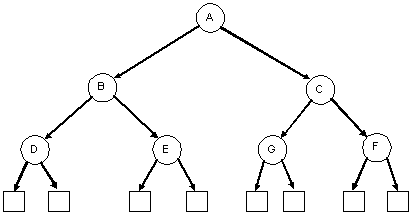
|
|---|
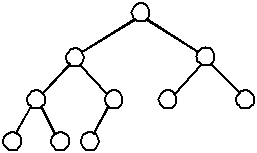
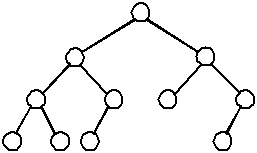
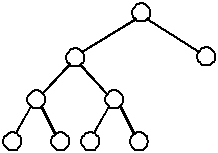
A complete binary tree is similar to a balanced binary tree except that all of the leaves must be placed as far to the left as possible. (The leaves must be "filled-in" from left to right, one level at a time.)
| A complete binary tree | An incomplete binary tree | An incomplete binary tree |
|
|
|
|---|
struct ListNode { ListNode *next; ListNode *prev; Data *data; };struct TreeNode { TreeNode *left; TreeNode *right; Data *data; };
Tree:
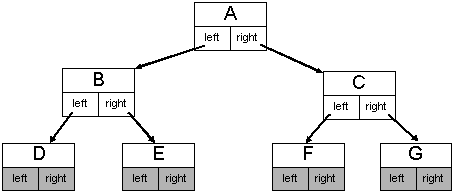
Linked list:

Self-check What is a binary tree? What is a balanced tree? What is a complete tree?
Traversing Binary Trees
Because trees are a recursive data structure, recursive algorithms are quite appropriate. In some cases, iterative (non-recursive) algorithms can be significantly more complicated.How would you traverse a linked list recursively? (How many ways can you traverse it?) Reminder: Traversing linked-list recursively.
| Recursive algorithm | Recursive algorithm with base case | |
|---|---|---|
|
|
Given these binary trees:
assume that visiting a node means printing the letter of the node. The result of the traversing the first tree is A in all 3 cases.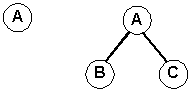
For the second tree, we have:
Self-check Perform the three different traversals on the tree below.
 |
| Modula-2 ©2008 |
Assuming that visiting a node means printing the letter of the node, what is the output for
An example of an expression tree: (order is important)
Self-check What kind of traversal would we use to evaluate the expression tree?
Implementing Tree Algorithms
struct Node
{
Node *left;
Node *right;
int data;
};
Node *MakeNode(int Data)
{
Node *node = new Node;
node->data = Data;
node->left = 0;
node->right = 0;
return node;
}
void FreeNode(Node *node)
{
delete node;
}
typedef Node* Tree;
int Count = 0;
Tree BuildBinTreePre(int height)
{
if (height == -1)
return 0;
Node *node = MakeNode('A' + Count++); // build the node
node->left = BuildBinTreePre(height - 1); // build the left tree
node->right = BuildBinTreePre(height - 1); // build the right tree
return node;
}
void main()
{
Tree t = BuildBinTreePre(1);
}
The name of the function tells us in which order this tree has been built (preorder).A / \ B C
How would we construct these trees?
Notice when the node/subtrees are being constructed:
B C
/ \ / \
A C A B
Tree BuildBinTreeIn(int height)
{
if (height == -1)
return 0;
Node *node = new Node;
node->left = BuildBinTreeIn(height - 1); // build left subtree
node->data = 'A' + Count++; // build node
node->right = BuildBinTreeIn(height - 1); // build right subtree
return node;
}
Tree BuildBinTreePost(int height)
{
if (height == -1)
return 0;
Node *node = new Node;
node->left = BuildBinTreePost(height - 1); // build left subtree
node->right = BuildBinTreePost(height - 1); // build right subtree
node->data = 'A' + Count++; // build node
return node;
}
Self-check: Suppose you used these functions to create a tree with height of 2. This would require 7 nodes and use the letters: ABCDEFG. What would the trees look like using: BuildBinTreePre? BuildBinTreeIn? BuildBinTreePost?
More Tree Algorithms
State the recursive algorithms for finding:
Definitions and sample implementations:
0 if the tree is empty 1 + if tree is not empty nodes in left subtree + nodes in right subtree
int NodeCount(Tree tree)
{
if (tree == 0)
return 0;
else
return 1 + NodeCount(tree->left) + NodeCount(tree->right);
}
Implementation #1: (naive, from the definition)-1 if the tree is empty (Definition) 1 + height of left subtree if height of left subtree > height of right subtree 1 + height of right subtree otherwise
int Height(Tree tree)
{
if (tree == 0)
return -1;
if (Height(tree->left) > Height(tree->right))
return Height(tree->left) + 1;
else
return Height(tree->right) + 1;
}
int Height(Tree tree)
{
if (tree == 0)
return -1;
int lh = Height(tree->left);
int rh = Height(tree->right);
if (lh > rh)
return lh + 1;
else
return rh + 1;
}
int Height(Tree tree)
{
if (tree == 0)
return -1;
else
return (1 + Max(Height(tree->left), Height(tree->right)));
}
Assume that "visting" a node simply means printing out the value of the data element:
void VisitNode(Tree tree)
{
cout << tree->data << endl;
}
Implementation #1 Implementation #2 void TraversePreOrder(Tree tree) { if (tree == 0) return; VisitNode(tree); TraversePreOrder(tree->left); TraversePreOrder(tree->right); } void TraverseInOrder(Tree tree) { if (tree == 0) return; TraverseInOrder(tree->left); VisitNode(tree); TraverseInOrder(tree->right); } void TraversePostOrder(Tree tree) { if (tree == 0) return; TraversePostOrder(tree->left); TraversePostOrder(tree->right); VisitNode(tree); }void TraversePreOrder(Tree tree) { if (tree) { VisitNode(tree); TraversePreOrder(tree->left); TraversePreOrder(tree->right); } } void TraverseInOrder(Tree tree) { if (tree) { TraverseInOrder(tree->left); VisitNode(tree); TraverseInOrder(tree->right); } } void TraversePostOrder(Tree tree) { if (tree) { TraversePostOrder(tree->left); TraversePostOrder(tree->right); VisitNode(tree); } }
Self-check Using the implementations above, what is the complexity for each of these traversal orders? In other words, how many nodes are visited? (How many times is each node accessed?)
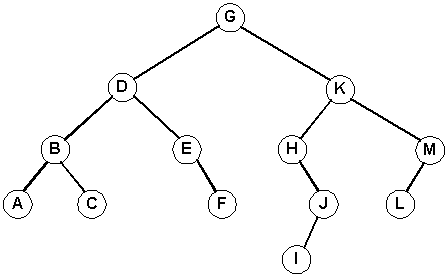
Level-Order Traversal
Traversing all nodes on level 0, from left to right, then all nodes on level 1 (left to right), then nodes on level 2 (left to right), etc. is level-order traversal.So, a level-order traversal of this tree:
 |
| Modula-2 ©2008 |
will result in the nodes being visited in this order:
G D K B E H M A C F J L I
Traversing in level-order really isn't any more complicated by definition:
The recursive definition:
If the level being visited is: 0 Visit the node
If the level being visited is: > 0 Traverse the left subtree in level order
Traverse the right subtree in level order
1. void TraverseLevelOrder(Tree tree)
2. {
3. int height = Height(tree);
4. for (int i = 0; i <= height; i++)
5. TraverseLevelOrder2(tree, i);
6. }
7. void TraverseLevelOrder2(Tree tree, int level)
8. {
9. if (level == 0)
10. VisitNode(tree);
11. else
12. {
13. TraverseLevelOrder2(tree->left, level - 1);
14. TraverseLevelOrder2(tree->right, level - 1);
15. }
16. }Details of the TraverseLevelOrder2 function above:
Level Nodes at level N Nodes in tree Node Accesses
------------------------------------------------------------
0 1 1 1
1 2 3 4
2 4 7 11
3 8 15 26
4 16 31 57
5 32 63 120
6 64 127 247
7 128 255 502
8 256 511 1013
9 512 1023 2036
10 1024 2047 4083
11 2048 4095 8178
12 4096 8191 16369
13 8192 16383 32752
14 16384 32767 65519
15 32768 65535 131054
16 65536 131071 262125
17 131072 262143 524268
18 262144 524287 1048555
19 524288 1048575 2097130
Self Check: Modify the algorithm above so it prints the nodes in reverse level-order:
I L J F C A M H E B K D G
| Pseudocode | ||
|---|---|---|
|

|
What is the complexity for this level-order traversal? How does the implementation of the Queue data structure affect the complexity?
Self Check: Implement a function similar to TraverseLevelOrder that uses a queue as an auxiliary data structure. The function won't be recursive.
Self Check: Implement a function similar to TraverseLevelOrder that uses a stack as an auxiliary data structure. The function won't be recursive. What order is this traversal?
Binary Search Trees
DefinitionA binary search tree (BST) is a binary tree in which the values in the left subtree of a node are all less than the value in the node, and the values in the right subtree of a node are all greater than the value of the node. The subtrees of a binary search tree must themselves be binary search trees. (Recursive)Note that under this definition, a BST never contains duplicate nodes.
Some operations for BSTs:
|
|
|
As always
Sample code for finding an item in a BST:
|
Sample code for inserting an item into a BST:
void InsertItem(Tree &tree, int Data)
{
if (tree == 0)
tree = MakeNode(Data);
else if (Data < tree->data)
InsertItem(tree->left, Data);
else if (Data > tree->data)
InsertItem(tree->right, Data);
else
cout << "Error, duplicate item" << endl;
}
Self Check: Create a tree using these values (in this order): 12, 22, 8, 19, 10, 9, 20, 4, 2, 6
What is the height of the resulting tree? What can you say about the tree? (Is it balanced? Is it complete?
If it is unbalanced, which nodes are out of balance?)
Self Check:
Create a tree using the same values but in this order: 2, 4, 6, 10, 8, 22, 12, 9, 19, 20
What is the height of the resulting tree? What can you say about the tree? (Is it balanced? Is it complete?
If it is unbalanced, which nodes are out of balance?)
Self Check: What is the worst case time complexity for searching a BST? Best? What causes the best/worst cases?
Self Check: Given a BST with 10 nodes, what is the maximum and minimum height of the tree? Suppose the BST had 20 nodes?
Self Check: Given a BST of height 2, what is the maximum and minimum number of leaves in the tree? What if the BST had a height of 3?
Deleting A Node
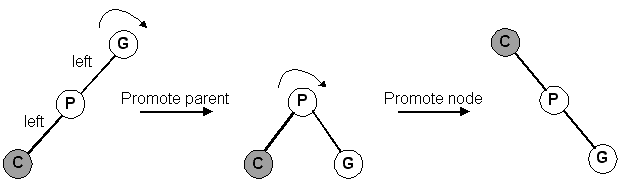
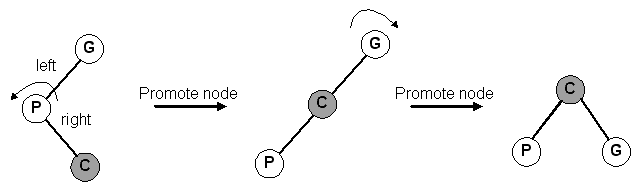
The caveat of deleting a node is that, after deletion, the tree must still be a BST. Using this tree as an example: |
| Modula-2 ©2008 |
This is trivial. Set the parent's pointer to this node to NULL.
Replace the deleted node with its right child. Note that this case can be combined with Case #1 by "promoting" the right child. This works even if the right child is NULL.
Similar to #2. Promote the left child.
 |
| Modula-2 ©2008 |
|
|
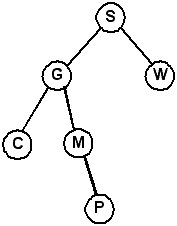
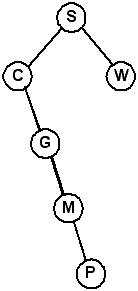
Self Check: What is the resulting tree from deleting the root node (G) in the tree above? What does the tree look like if you delete K from the tree?
Rotating Nodes
Note: An important property of rotation is that after the rotation, the sort order is preserved. This is important, because the resulting tree must still be a BST.
Rotate right about the root, S. (Same as promoting the left child, M)
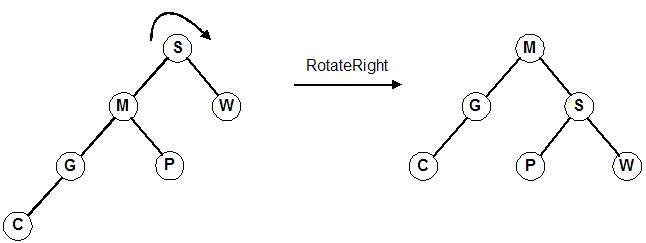
Rotate left twice about the root. (Far right diagram) First rotate about 1, then rotate about 3. (Same as promoting 3 and then promoting 6)
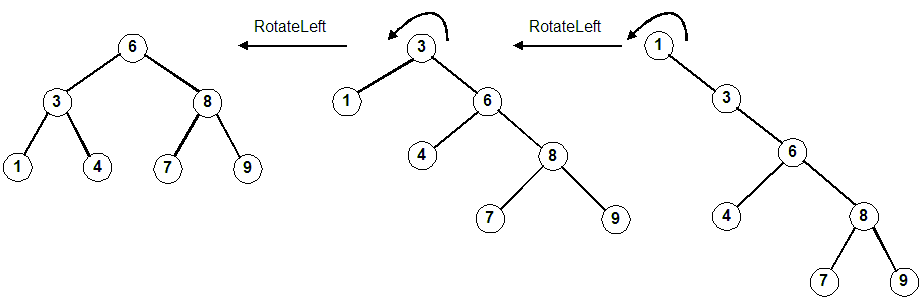
Using the defintions above. Note the parameter to each function is a reference to a pointer.
Follow the four lines of code in this example. We are rotating right about S (promoting M).
Rotating a tree right Rotating a tree left void RotateRight(Tree &tree) { Tree temp = tree; tree = tree->left; temp->left = tree->right; tree->right = temp; }void RotateLeft(Tree &tree) { Tree temp = tree; tree = tree->right; temp->right = tree->left; tree->left = temp; }
1. temp = Tree; // temp ===> S 2. tree = temp->left; // tree ===> M 3. temp->left = tree->right; // temp->left ===> P 4. tree->right = temp; // tree->right ===> S
Adjusting the diagram: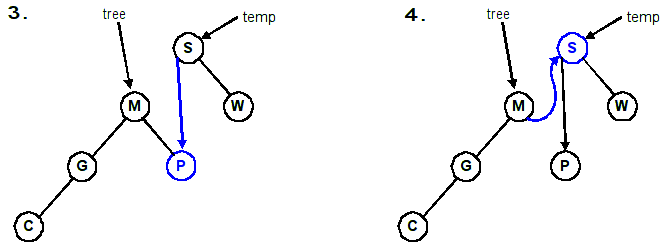
Note that these four trees below all contain the same data.You can easily see why we passed a reference (or pointer) to the root of the tree. If you just pass the pointer itself (by value), after the rotation tree still points at node S, which is wrong. Keep this in mind when you are implementing the tree functions.
| One | Two | Three | Four |
|---|---|---|---|
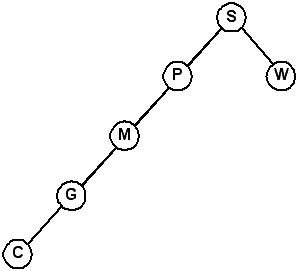
|
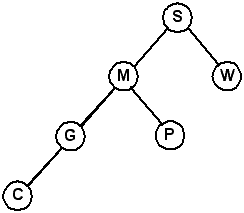
|
|
|
Can you explain why there are four different representations for the same data?
Self Check: What is the resulting tree from rotating left about the root node (G) in the tree below? How about rotating right about the root? Rotating left about a node means promoting the node's right child. Rotating right about a node means promoting the node's left child.
 |
| Modula-2 ©2008 |
Self Check: After rotating right about G above, the tree is unbalanced because at least one node is unbalanced. Specifically, which nodes are unbalanced?
Self Check: Insert the letters: P I N K F L O Y D E R S into a BST. What is the height of the tree? The tree is NOT balanced. Which nodes in the tree are unbalanced? Rotate about the root (P) node. Now what is the height of the tree? Which nodes are unbalanced now? Finally, delete node P from the original tree.
Self Check: Insert the letters: K E Y B O A R D I S T into a BST. What is the height of the tree? The tree is NOT balanced. Which nodes in the tree are unbalanced? Rotate about the root (K) node. Now what is the height of the tree? Which nodes are unbalanced now? Finally, delete node E from the rotated tree.
Self Check: Insert the letters: K E Y B O A R D I S T into a BST. What is the sequence of letters when doing a Pre-order traversal? An In-order traversal? A Post-order traversal?
Splay Trees
Invented by D.D. Sleator and R.E. Tarjan in 1985.Left-Left orientation (zig-zig)
Left-Right orientation (zig-zag)
Right-Right orientation (zig-zig)
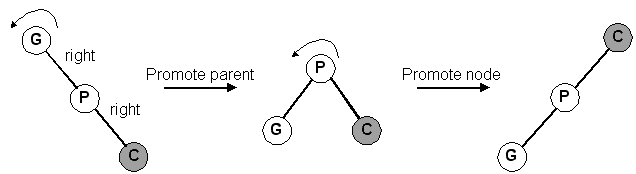
Right-Left orientation (zig-zag)
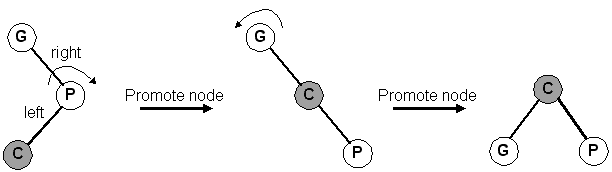
Our orientation with our grandparent is left-right at first:
Now, our orientation with our grandparent is left-left: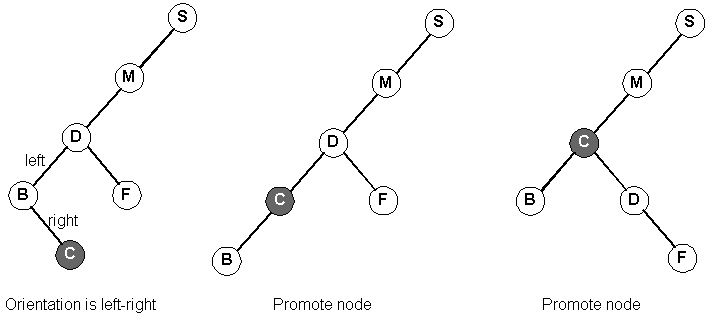
The result of splaying F to the root: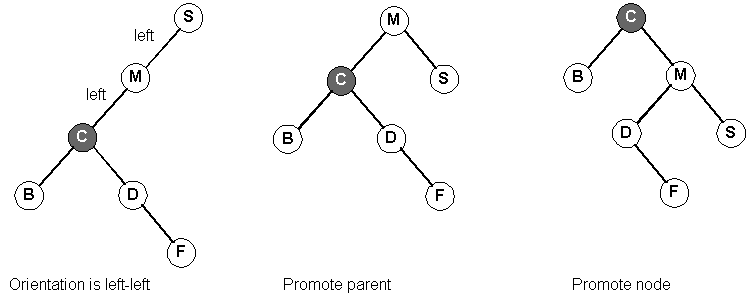
Additional Notes: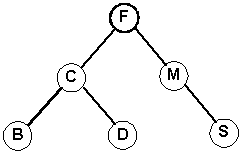
Given this expression:
The result after evaluation is 56. The tree that represents it looks like this:(7 + 5) * (3 + 4) - (4 * (9 - 2))
Operators are always internal nodes and operands are always external (leaf) nodes.
(7 + 5) * (3 + 4) - (4 * (9 - 2))
^ ^ ^
| | |
| | |
root of root root of
left subtree right subtree
Evaluating the tree gives the same result. Evaluating an expression tree simply means reducing each subtree by post-order traversal. Why post-order?
Self-Check: Perform a post-order traversal on the expression tree above. This will create a postfix expression. Using the stack method from here, evaluate it and verify that you get the value 56.
<expression> ::= <term> { <addop> <term> }
<term> ::= <factor> { <mulop> <factor> }
<factor> ::= ( <expression> ) | <identifier> | <literal>
<addop> ::= + | -
<mulop> ::= * | /
<identifier> ::= a | b | c | ... | z | A | B | C | ... | Z
<literal> ::= 0 | 1 | 2 | ... | 9
Our "language" consists of the following tokens:
Examples:Valid tokens: ()+-*/abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789
Valid expressions: A, B, 1, A + 2, A + B, A * (B), A * (B - 2), (1) Invalid constructs: AB, 3A, 123, A(3), A + (), A * -3
Given any infix valid expression within the language, we can evaluate or reduce the expression in a two-step process:
<expression> ::= <term> { <addop> <term> }
<term> ::= <factor> { <mulop> <factor> }
<factor> ::= ( <expression> ) | <identifier> | <literal>
MakeExpression(Tree)
1 Make a term, setting Tree to point to it
2 while the next token is '+' or '-'
3 Make an operator node, setting left child to Tree and right to NULL. (Tree points to new node)
4 Get the next token.
5 Make a term, setting the right child of Tree to point to it.
6 end while
End MakeExpression
MakeTerm(Tree)
7 Make a factor, setting Tree to point to it
8 while the next token is '*' or '/'
9 Make an operator node, setting left child to Tree and right to NULL. (Tree points to new node)
10 Get the next token.
11 Make a factor, setting the right child of Tree to point to it.
12 end while
End MakeTerm
MakeFactor(Tree)
13 if current token is '(', then
14 Get the next token
15 Make an expression, setting Tree to point to it
16 else if current token is an IDENTIFIER
17 Make an identifier node, set Tree to point to it, set left/right children to NULL.
18 else if current token is a LITERAL
19 Make a literal node, set Tree to point to it, set left/right children to NULL.
20 end if
21 Get the next token
End MakeFactor
GetNextToken
while whitespace
Increment CurrentPosition
end while
CurrentToken = Expression[CurrentPosition]
Increment CurrentPosition
End GetNextToken
<expression> ::= <term> { <addop> <term> }
<term> ::= <factor> { <mulop> <factor> }
<factor> ::= ( <expression> ) | <identifier> | <literal>
Diagrams for the expression: A + B (All addresses are arbitrary, but represent the order the nodes were created.)
A A + A + B 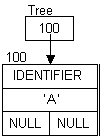
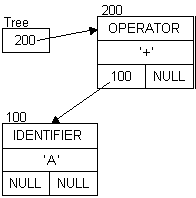
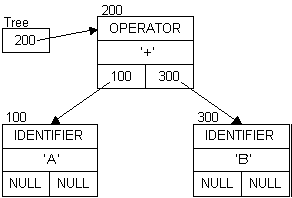
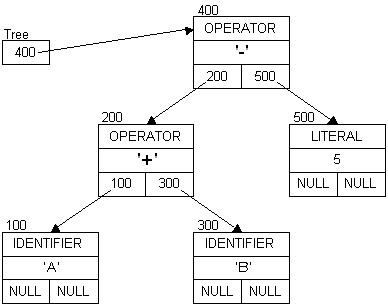
Extending the expression to: A + B - 5
A + B - A + B - 5 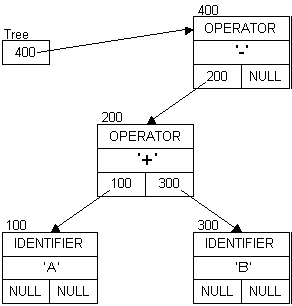
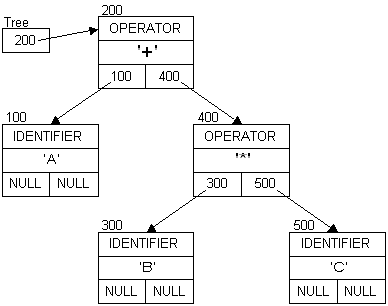
Diagrams for the expression: A + B * C
A + B as before:
Adding: * C
A + B * A + B * C 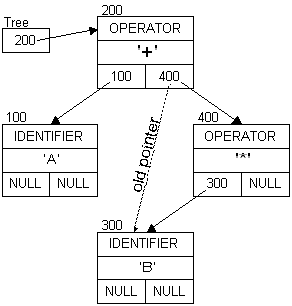
Some simplification examples:
4 * (2 + 3) → 20 A * (2 + 3) → A * 5 A * (3 - 4 + 1) + B → B A + 2 * 3 → A + 6
Simplification Rules:
| Condition | Action |
|---|---|
| Both children are LITERAL | Evaluate the expression and promote the result to the node that contained the operator. 0 / 0 → (exception) |
| The left child is a LITERAL and the right child is an IDENTIFIER or OPERATOR (expression). |
If expression is one of these forms, it can be simplified and the result promoted:
0 + E → E 1 * E → E 0 * E → 0 0 / E → 0 |
| The right child is a LITERAL and the left child is an IDENTIFIER or OPERATOR (expression). |
If expression is one of these forms, it can be simplified and the result promoted:
E + 0 → E E - 0 → E E * 0 → 0 E * 1 → E E / 1 → E E / 0 → (exception) |
| Both children are IDENTIFIER. |
If expression is one of these forms, it can be simplified and the result promoted:
I - I → 0 I / I → 1 |
Example of the form: E - 0 → E
Caveats
This technique will not be able to simplify all expressions. For example, these can not be simplified:
To simplify these expressions, more complex algorithms are needed. One step is to normalize the expressions such that different operand orderings can be dealt with. For example, sorting the identifiers in alphabetical order:(A + 7) / (A + 7) # should be 1 (A + 7) - (A + 7) # should be 0 (A + 7) - (7 + A) # same (3 + A + 4) - (A + 7) # same (A + B + C) - (C + B + A) # same
The resulting tree:(A + C + B) ==> (A + B + C) (C + B + A) ==> (A + B + C) (B + A + C) ==> (A + B + C)
Then, you'd have to recognize that the entire left subtree of the root is identical to the entire right subtree of the root. You would do this with a recursive algorithm that determines if two trees are identical. The Poor-Man's Way™ is to simply perform a traversal (pre-, post-, in-order, doesn't matter) and compare the outputs.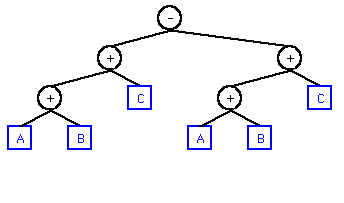
A possibly more elegant solution would be a simple recursive function. Here's a prototype:
// From the example code above
struct Node
{
Node *left;
Node *right;
int data;
}
bool isIdentical(const Node *left_tree, const Node *right_tree);
This requires much more sophisticated logic (in the general case) to make sure that the transformations do not change the underlying meaning. This is non-trivial for dealing with arbitrarily complex expressions.(A * C + B) ==> (A * B + C) # incorrect (C - B - A) ==> (A - B - C) # incorrect
Self-check Build the parse tree for these expressions:
A + B + C A + B * C A * B + C (A + B) * C A * (B + C) |
Self-check Given the expression tree below, show the postfix expression. Hint: perform a post-order traversal.
Real World: Compilers and Constant Folding
This is how compilers do constant folding. They simply make a tree out of the expression and perform a post-order traversal to evaluate it at compile time.Given this code (from the link above):In the olden days, compilers only did this for literals and compile-time constants because the values had to be known to the compiler. Nowadays, compilers are much smarter and can analyze the code to determine that some variables never change their values.
int main()
{
// a, b, and c are variables, not constants!
int a = 30;
int b = 9 - (a / 5); // b is 3
int c;
c = b * 4; // c is 12
if (c > 10) // 12 > 10 (true)
{
c = c - 10; // c is 12 - 10, which is 2
}
return c * (60 / a); // return 2 * (60 /30) ==> 2 * 2 ==> 4
}
No optimization Optimization -O
Note that if this is not main but some other function that returns an integer, and the entire body of the function is being reduced to this:
The compiler may just remove the call to the function altogether. This means that client code could be reduced from this (assume the function is named foo):return 4;
to this:int x = foo();
int x = 4;
// a, b, and c are now global
int a = 30;
int b = 9 - (a / 5); // b is 3
int c;
int main()
{
c = b * 4; // c is 12
if (c > 10) // 12 > 10 (true)
{
c = c - 10; // c is 12 - 10, which is 2
}
return c * (60 / a); // return 2 * (60 /30) ==> 2 * 2 ==> 4
}
If we declare them as static:
// a, b, and c are now static (file-scope)
static int a = 30;
static int b = 9 - (a / 5);
static int c = b * 4;
int main()
{
if (c > 10)
{
c = c - 10;
}
return c * (60 / a);
}
If we compile with -O2, we see this slightly more optimized version (without the redundant load of c):main: movl _ZL1c(%rip), %eax ; put c in eax cmpl $10, %eax ; compare c with 10 jle .L2 ; if less-than or equal, jump to L2 subl $10, %eax ; c is greater than 10, so subtract 10 movl %eax, _ZL1c(%rip) ; put eax back into c .L2: movl _ZL1c(%rip), %eax ; put c in eax addl %eax, %eax ; c + c, same as c * 2 ret
However, if I add this before mainmain: .LFB0: movl _ZL1c(%rip), %eax cmpl $10, %eax jle .L2 subl $10, %eax movl %eax, _ZL1c(%rip) .L2: addl %eax, %eax ret
void foo()
{
extern int i;
a = i;
}
static void foo()
{
extern int i;
a = i;
}
int main()
{
foo();
if (c > 10)
{
c = c - 10;
}
return c * (60 / a);
}
Suppose we really didn't want the compiler to optimize the local variables as in the original code. How could we tell the compiler not to optimize the variables a, b, and c? (Obviously, we would just omit the -O2 compiler option, but that will disable ALL optimizations, we just want to disable the ones on the local variables.)
This is the way:
int main()
{
// a, b, and c will not be optimized
volatile int a = 30;
volatile int b = 9 - (a / 5); // b is 3
volatile int c;
c = b * 4; // c is 12
if (c > 10) // 12 > 10 (true)
{
c = c - 10; // c is 12 - 10, which is 2
}
return c * (60 / a); // return 2 * (60 /30) ==> 2 * 2 ==> 4
}
How about this code?
void foo(int &x); // prototype
int main()
{
int a = 30;
int b = 9 - (a / 5); // b is 3
int c;
foo(a);
foo(b);
// The code below will not be optimized because
// foo has indicated it will modify a and b.
c = b * 4; // c is 12
if (c > 10) // 12 > 10 (true)
{
c = c - 10; // c is 12 - 10, which is 2
}
return c * (60 / a); // return 2 * (60 /30) ==> 2 * 2 ==> 4
}
no optimization takes place. This should give you some insight into how much compilers have improved over the years when it comes to performing deep analysis of the code.void foo(const int &x); // prototype
The compilers used are version 5.1 (April 2015) and 5.3 (December 2015). Newer compilers
may do even better with the optimizations.